And thinking some more about Caitlin's observation:
Consider that -1 = Exp[Pi I], then an nth root of -1 is Exp[Pi I / n].
The n nth roots of unity are given by Exp[2 Pi I k / n] with k from 1 to n. (de Moivres numbers)
Multiplying the nth root of -1 by these gives the n nth roots of -1 as Exp[(2k+1) Pi I / n], again with k from 1 to n.
Since any negative number -N (N positive) can be written as -1*N, we have the nth root as the principal root of N multiplied by these n roots of -1.
Here, for example, are nine 9th roots of -1:
In[1]:= rootOfMinusOne[k_, n_] := Exp[(2 k + 1) Pi I/n] In[2]:= roots9 = Table[rootOfMinusOne[k, 9], {k, 9}] Out[2]= {E^((I \[Pi])/3), E^((5 I \[Pi])/9), E^(( 7 I \[Pi])/9), -1, E^(-((7 I \[Pi])/9)), E^(-((5 I \[Pi])/9)), E^(-(( I \[Pi])/3)), E^(-((I \[Pi])/9)), E^((I \[Pi])/9)} In[3]:= #^9 & /@ roots9 Out[3]= {-1, -1, -1, -1, -1, -1, -1, -1, -1} In[4]:= cPlot[lst_, opts___] := ListPlot[{Re[#], Im[#]} & /@ lst, AspectRatio -> 1, AxesLabel -> {"Re", "Im"}, opts] In[5]:= cplt = cPlot[roots9, PlotLabel -> "The nine 9th roots of -1"] 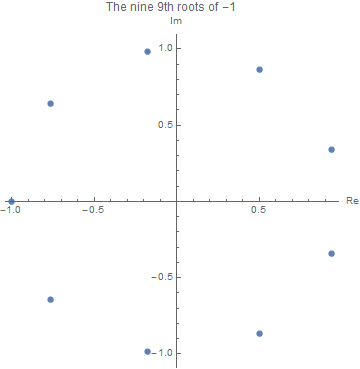
 Message Boards
Message Boards 
0 Response to "Getting Complex Answers From Mathematica Solve"
Post a Comment